NOTE: This page uses MathJax, a JavaScript program running in your web browser, to render equations. It renders the equations in three steps: 1. during loading you may see the “raw code” that generates the equations, 2. an HTML version of the equations is pre-rendered (functional, but not nice looking), then 3. a full and proper “typeset” rendering of the equations. Depending on the speed of your system and browser, it may take a few seconds to tens of seconds to finish the whole process. The end product is usually worth the wait, imho.
This is the next instalment in Phelonius’ Pedantic Solutions which aims to tackle something I wish I had when I was doing my physics degree: some step-by-step solutions to problems that explained how each piece was done in a painfully clear way (sometimes I was pretty thick and missed important points that are maybe obvious to me now, looking back). I have realized I could have benefited from a more integrated approach to examples, where whatever tools that are needed are explained as the solution is presented, so that is at the core of these attempts. I have also been told all my life that the best way to learn something is to try to teach it to someone else, and so this is part of my attempt to become more agile and comfortable with the ideas and tools needed to do modern physics. If you don’t understand something, please ask, because I haven’t explained it well enough and others will surely be confused as well.
Things covered:
- Cosmic rays and detectors
- Probability Density Functions (PDFs)
- Cumulative Distribution Functions (CDFs)
- Inverting functions
- Monte-Carlo simulations
- Geometric and trigonometric identity proofs
- You were probably lied to
Cosmic rays have always fascinated me. I had the chance, once upon a time, to work on a scientific payload proposal for a student-run CubeSat satellite design (part of the 1st Canadian Satellite Design Challenge), and I jumped at the chance. What I present here is part of that effort. I had previously worked on three cosmic ray experiments as an undergraduate (with my electronics and software development experience mostly… I am still but a larval physicist): two versions of a system that used naturally occurring cosmic rays to produce tomographic images of whatever was inside (3D images like a CT scan), and another to observe changes in the intensity and direction of cosmic rays using a solar weather observatory I mostly built (I had to move, 6 bricks at a time on a hand truck, 2.4 metric tonnes of lead as shielding from another building across campus, ugh, worst summer job ever but the results were worth it).
As part of the satellite payload design, I built a proof-of-concept cosmic ray detector out of mostly scrap I was able to scrounge together (and a few basic supplies I had to buy). The cosmic ray detector consisted of two 1/2″ thick, 15cm x 15cm plastic scintillator panels instrumented with photomultiplier (PMT) tubes. Every time an ionizing particle goes through one of the scintillator panels, it gives off a trail of photons, some of which hit the face of the PMTs which are sensitive enough to pick up single photons and generate an electrical pulse in response. These panels were separated by 1.0m and had 15cm of lead bricks between them. Note: the lead bricks block any local radiation from radioactive sources in the environment, but most cosmic rays pass right through them. If the PMT on only one scintillator is activated, that event is ignored (either it was noise from the PMT, local radiation not powerful enough to go through the lead, or a cosmic ray that didn’t go through both panels because of its path); but if it goes through both scintillators (and the lead between them and fires both associated PMTs), then that event is counted.
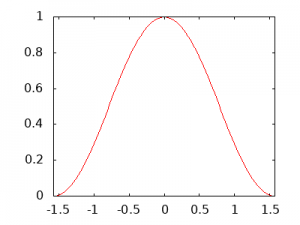
So here’s the problem… I needed to know how many cosmic rays to expect to pass through both scintillator panels of my detector. Once I knew that, I could compare that with the number I actually got from the experimental apparatus, and that would let me know how good the scrap detector I had built was. There is an excellent free resource on cosmic ray physics (and so much other physics) in the Particle Data Group’s “Review of Particle Physics”. The whole thing is here, but the sub-section on cosmic ray physics is here (note, this link is to a PDF document). As an aside, you can order a print copy of this massive publication for free no matter where you live (or download the whole thing as a PDF), it’s pretty boffo. Here’s the tl;dr version for this solution: if you hold your thumb nail horizontally, about one cosmic ray passes through your thumbnail (and every other part of your body) every minute… the rate is about 1 per square centimetre per minute (and they are mostly made of muons and their energy is 3GeV on average if that’s of any use to you). Cosmic rays mostly come from directly overhead, but they can be from any direction of the sky and follow, roughly, a \(cos^{2}(\theta)\) probability distribution (see diagram, note that the x-axis is from \(-\pi/2\) through \(\pi/2\), but expressed as a decimal number). This means that the relative probability of a cosmic ray coming from any particular angle relative to directly upwards can be calculated by plugging that angle into \(cos^{2}(\theta)\), e.g. at \(\theta = 0\) radians (\(0^\circ\)) from vertical, \(cos^{2}(0) = 1\); but at \(\theta = \pi/3\) radians (\(60^\circ\)) from vertical (\(\pi/6 = 30^\circ\) up from from the horizon), there’s a 75% smaller chance of a cosmic ray from that angle since \(cos^{2}(\pi/3) = 0.25\).
This all comes back to the detector in trying to figure out what percentage of the cosmic rays hitting the top scintillator also hit the bottom panel (did I mention I stood it on its side so that one scintillator panel was directly above the other one?). Since the panels are 15cm x 15cm, I would expect roughly (very roughly) 225 cosmic rays per minute (15cm x 15cm x 1 cosmic ray per square centimetre per minute) to hit the upper surface of the top panel, which is very roughly about 4 per second. But only those cosmic rays that go through both scintillator panels is counted as an “event”. I tried to calculate what’s called the solid-angle acceptance of the detector for the given angular distribution of cosmic rays, but my brain broke and it looked like trying to calculate it directly was way more trouble than it was worth (if you have a way of doing this, please share your solution, it got nasty pretty quick for me).
An easier way to tackle this kind of problem is to write a Monte Carlo simulation (named after a city renowned for its gambling, and thus its association with random numbers). I’ll perhaps go into the nitty gritty another time, but in this case it involves randomly and uniformly picking an X/Y coordinate for the cosmic ray to pass through the top scintillator panel (the cosmic ray is equally likely to pass through any point on its surface), a uniformly distributed random direction to come from relative to the horizontal (a \(2\pi\) radians = 360° circle, think degrees from north), and then randomly picking the angle (relative to vertical) the cosmic ray came from to hit that X/Y location. The trick with the last part is that computers are really good at picking uniform random numbers (where any random value is as likely as any other random value within the range they are being generated over), but they don’t tend to have the ability to pick a random number according to any other non-uniform probability function. To make this work then, I needed to figure out a way of converting from a uniform random number into a \(cos^{2}(\theta)\) distribution. I learned how to do this in a 4th year Computational Physics course (PHYS4807 at Carleton University in Ottawa, Canada) that was a triple-headed monster in that it taught C++ (I was good there, most were not), complex statistical methods as used in advanced particle physics in the real world (the first time any of us had seen anything that complex in terms of statistical analysis), and did it using the ROOT scientific computing program from CERN (which nobody knew). Note: ROOT is free to download and use, is an incredibly powerful scientific computing framework, and is used by ATLAS and other experiments at CERN to do analysis.
Once I had a simulated cosmic ray passing through the top panel (at a particular point, from a particular direction, at a particular angle relative to the vertical), I calculated whether it would hit the bottom panel if it continued in a straight line (not a bad assumption for cosmic rays, fyi). If it did, then I counted it as an event. By doing random generation of virtual cosmic ray events, I just had to run the simulation long enough to get a very accurate estimation of what percentage of cosmic rays hitting the top panel went through both panels. Since I knew from observed physics how often a particle should hit the top panel, and then “observing” the percentage of those that passed through both panels from the simulation, I would be able to estimate the number cosmic ray events in my real detector and see if my real measurements were close at all.
The process of allowing the computer to generate an arbitrary (non-uniform) random distribution consists of three phases:
- Determine the Probability Density Function (PDF)
- Calculate the Cumulative Distribution Function (CDF) from the PDF
- Invert the CDF to get the formula
The equation derived in the last step is what is used to convert from a uniform distribution like computer-generated random numbers into the distribution specified by the PDF, which is \(cos^{2}(\theta)\) in this case.
We know already that the relative probability of a cosmic ray coming from any particular angle off of vertical is \(cos^{2}(\theta)\) (from experimental results, sort of… that is a simplification but good enough for this application). But how to convert that into a proper PDF? The key is the notion of “probability”, and specifically if a cosmic ray is observed it had to come from somewhere (some angle). When the relative probabilities are added up for every possible angle, we need to get 100% (again, it just says that all events came from some angle, so the probabilities all add up to 1 = 100%). Since the angle, \(\theta\), is a continuous variable (it is a real number), when we integrate the PDF over its angular range the solution must be 1. This process is called normalization (so the probability of an observed cosmic ray coming from somewhere is 100%). The function \(cos^{2}(\theta)\) is unnormalized since taking its integral from \(-\pi/2\) to \(\pi/2\) results in a value greater than 1 (a probability greater than 100% is a nonsensical concept). To normalize the PDF, a normalization constant is put into the probability function (I use \(A\) in this case), then that constant is calculated by doing the integral (to which we know the solution we must get). Note that sometimes the normalization constant could be 1, but it may not be obvious before doing the integration, so the integration required to do the normalization is generally a required step. The normalized PDF has the following form:
\[ f(\theta) = A\cdot cos^{2}(\theta)\tag{1} \]
Remember that if \(f(\theta) = A\cdot cos^{2}(\theta)\), then \(f(\diamond) = A\cdot cos^{2}(\diamond)\) since \(\theta\) is just a symbol and can be replaced with anything as long as the new symbol is carried through the whole equation. To fully determine the PDF, we need to figure out the value of \(A\) in the following (I’ll talk about the \(\theta’\) stuff below).
\[ \int_{\theta’ = -\pi/2}^{\theta’ = \pi/2} f(\theta’)\, d\theta’ = \int_{-\pi/2}^{\pi/2} A\cdot cos^{2}(\theta’)\, d\theta’ = 1\tag{2} \]
where the range of the integral, \(-\pi/2\) through \(\pi/2\) just provides a \(\pi\) radians (180°) range from horizon to horizon with \(\theta = 0\) being directly overhead. Again, it is equal to \(1\) because once all the probabilities are added up (integrated in this case), the result must be 100%. Cosmic rays don’t travel through the Earth very far, so they generally don’t come from below the horizon in any significant number. I could have limited the angular range of the integral even further because of the geometry of my detector (two detector panels, one above the other), but I wanted to make a generic “cosmic ray generator” that I could use in other applications. Conversely, if I needed to generate a very large number of potential cosmic ray events, it would save computing power to have tailored the simulation to my specific detector. That was not necessary here: it’s a small detector, there are relatively few events, and I have lots of idle computing power on my desk.
Why the \(\theta’\) in the integrals? Well, it’s not strictly needed here because there would be no confusion between the integration variable (sometimes called the dummy variable) and the actual variable we care about (which is what specifies the limits on the integral). However, if there is an actual variable in the limits, which often happens and there will be when we calculate the CDF, there can be confusion about what is the integration variable and what is a limit if there is no way to glance at the equation and tell (it’s usually possible to figure out from context, but it just increases the chances of a mistake). As I have said in previous posts, the integration variable is irrelevant because it gets replaced with the limits during the evaluation phase and just disappears. This whole idea of “priming” integration variables (using it as a dummy variable) is common but really confused the heck out of me when I was learning. Now that I have (mostly) figured out why it is done, I just think of it in an abstract way. For instance, I could just as easily have written it with \(\oplus\) instead of \(\theta’\), and we would get the exact same answer at the end:
\[ \int_{\oplus = -\pi/2}^{\oplus = \pi/2} f(\oplus)\, d\oplus = \int_{-\pi/2}^{\pi/2} A\cdot cos^{2}(\oplus)\, d\oplus = 1\tag{2} \]
The reason for putting primes on the variable that underlies the calculation is that it helps remember what the equation is about, but also reminds us that it’s just an integration (aka dummy) variable. If we’re calculating stuff related to angles, then \(\theta’\) reminds us of that. Something like \(\oplus\) does the job (and explicitly reminds us that it’s a dummy variable), but it is completely abstract and provides no hint as to what we’re working with. Every scrap of information and/or structure can potentially help when working on a problem, so it is best not to deliberately toss any away if it can be helped. To that end, when I’m using \(\theta\) (or anything) as an integration variable, I will try to remember to put a “prime” on it here, but will continue to simply use \(\theta\) when I’m talking about angles.
It’s easy to integrate \(cos(\theta)\), but \(cos^{2}(\theta) = cos(\theta)\cdot cos(\theta)\)? That integral is hard to solve as-is (yeah, it can be looked up in a table or solved online, but the idea here is to solve it ourselves). Is there any way to get rid of the squared trigonometric function? The answer is yes, but it’s non-obvious in that you’re only likely to know about it if you’ve seen the necessary trigonometric identity before. I will derive that identity below since it’s good practice (and is a bit of an art form), but here’s the spoiler:
\[\int_{-\pi/2}^{\pi/2} A\cdot cos^{2}(\theta’)\, d\theta’ = \int_{-\pi/2}^{\pi/2} A\cdot \frac{1 + cos(2\theta’)}{2} d\theta’ = 1 \]
This integral is quite easy to do because the \(1/2\) and \(A\) can be brought outside the integral since they are both constant, and the remaining piece can be broken into the sum of two integrals because integration is a linear operator (more on this below).
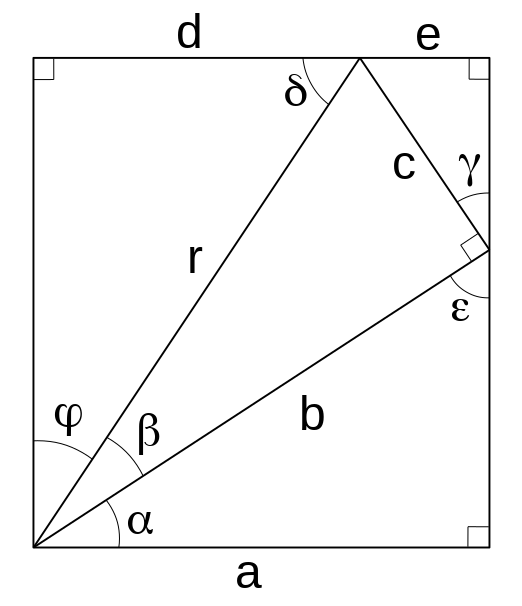
The diagram here can be used to prove the two common trigonometric identities that I needed to derive the other identity I used in solving this integral (there are so many ways to solve the integral, this was the one that came to mind for me). On the diagram, lengths are labelled with roman letters and angles are labelled with greek letters. Trigonometric identities are simply some statement about trigonometry is equal to some other statement about trigonometry, and they are usually derived by using other known properties of trigonometry. The fewer the assumptions, the more fundamental the identity; however, new identities are built out of more fundamental ones that have been proven, so answers to trigonometric questions can be answered with rigorous proofs using identities that have already themselves been rigorously proven. It can be quite fun to do this, but it can also be crazy-making if the path forward is not obvious. This is one of the branches of math where artistry and intuition, along with experience and a command of many techniques, is required to get solutions. There is no such thing in deriving identities as “plug and chug” solutions, and each requires some degree of insight.
Two assumptions that will be used in the proofs are the definitions of the sine and cosine functions. A quick reminder of another definition though: a right triangle is a triangle that has one of its angles as \(\pi/2\) radians (90°), a right angle. The sine of one of the non-right angles in a right triangle is the ratio of the length of the side opposite that angle divided by the length of the hypotenuse (the side opposite the right angle). The cosine of one of the non-right angles in a right triangle is the ratio of the length of the non-hypotenuse side adjacent to the angle divided by the length of the hypotenuse. The other assumption used in one of the proofs is the Pythagorean theorem that states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of both other sides. Using the off-kilter right angle triangle in the middle of the rectangle here, these can be expressed mathematically as:
\[ sin(\beta) = \frac{c}{r}\ \ \ \ \ \ cos(\beta) = \frac{b}{r}\ \ \ \ \ \ r^{2} = b^{2} + c^{2} \]
The first necessary identity is one I have seen used just about everywhere, and it has to do with squared trigonometric functions (like we’re dealing with). Looking at the right triangle inside the rectangle whose sides are of length \(b\), \(c\), and \(r\):
\[ sin(\beta) = \frac{c}{r}\,\rightarrow\, c = r\cdot sin(\beta)\ \ \ \ \ \ cos(\beta) = \frac{b}{r}\,\rightarrow\, b = r\cdot cos(\beta) \]
Using the Pythagorean theorem and substituting the above:
\[ r^{2} = b^{2} + c^{2}\,\rightarrow\, r^{2} = \left(r\cdot cos(\beta)\right)^{2} + \left(r\cdot sin(\beta)\right)^{2} \]
Doing the squares, dividing it all by \(r^{2}\), and re-arranging slightly:
\[ \frac{r^{2}}{r^{2}} = \frac{r^{2}\cdot cos^{2}(\beta)}{r^{2}} + \frac{r^{2}\cdot sin^{2}(\beta)}{r^{2}}\,\rightarrow\, cos^{2}(\beta) + sin^{2}(\beta) = 1 \]
Which is the standard form of this important trigonometric identity. Solving for the value we are dealing with in the integral, we get:
\[ cos^{2}(\beta) = 1\, – sin^{2}(\beta)\tag{3} \]
We still have a \(sin^{2}(\beta)\) so it may not look like we’re any further ahead, but there’s another identity that will allow us to get rid of it, which I will derive now. This proof, including the diagram above, is based on an excellent video presentation by Linda Green titled “Proof of the Angle Sum Formula” [1]. We will need the solutions for the lengths of right triangle sides \(b\) and \(c\) relative to angle \(\beta\) from above. We also need the following observations about various labelled angles. Recall that the angles of any triangle on a plane (flat surface) always add up to \(\pi\) radians (180°), and that a right angle is \(\pi / 2\) radians (90°). We get:
\[ \epsilon = \pi – \frac{\pi}{2} – \alpha = \frac{\pi}{2} – \alpha \]
which is just the total sum of the angles of the triangle, \(\pi\), minus the right angle, \(\pi/2\), minus the other angle in the triangle, \(\alpha\), and leaves the size of the angle \(\epsilon\). Similarly:
\[ \gamma = \pi – \frac{\pi}{2}\, – \epsilon = \frac{\pi}{2}\, – \epsilon = \frac{\pi}{2}\, – \left(\frac{\pi}{2}\, – \alpha\right) = \frac{\pi}{2}\, – \frac{\pi}{2} + \alpha = \alpha \]
Here it’s done a little differently in that we know that the angle \(\epsilon\) plus the angle \(\gamma\) plus the right angle, \(\pi/2\), sandwiched between them add up to \(\pi\) because they add up to a straight line (which is \(\pi\) radians, 180°). Then we can observe that (with some substitution, re-arranging, and remembering we have shown that \(\gamma = \alpha\)):
\[ sin(\gamma) = sin(\alpha) = \frac{e}{c}\,\rightarrow\, e = c\cdot sin(\alpha) = [r\cdot sin(\beta))]\cdot sin(\alpha) = r\cdot sin(\alpha)\cdot sin(\beta) \]
\[ cos(\alpha) = \frac{a}{b}\,\rightarrow\, a = b\cdot cos(\alpha) = [r\cdot cos(\beta)]\cdot cos(\alpha) = r\cdot cos(\alpha)\cdot cos(\beta) \]
Following the same sort of logic:
\[ \psi = \frac{\pi}{2}\, – \alpha\, – \beta \]
\[ \delta = \pi\, – \frac{\pi}{2}\, – \psi = \frac{\pi}{2}\, – \left(\frac{\pi}{2}\, – \alpha\, – \beta\right) = \frac{\pi}{2}\, – \frac{\pi}{2} + \alpha + \beta = \alpha + \beta \]
Then:
\[ cos(\delta) = cos(\alpha + \beta) = \frac{d}{r}\,\rightarrow\, d = r\cdot cos(\alpha + \beta) \]
Since the line \(d e\) is parallel with line \(a\) (i.e. \(de \parallel a\)), and they are the same length since they are opposite sides of a rectangle, then substituting:
\[ a = d + e\,\rightarrow\, r\cdot cos(\alpha)\cdot cos(\beta) = r\cdot cos(\alpha + \beta) + r\cdot sin(\alpha)\cdot sin(\beta) \]
Then dividing both sides by \(r\) and re-arranging:
\[ cos(\alpha + \beta) = cos(\alpha)\cdot cos(\beta)\, – sin(\alpha)\cdot sin(\beta)\tag{4} \]
Which is the second standard identity we needed to derive. As indicated above, this one is the “sum of angles” identity. If we let \(\alpha = \beta = \theta\), then \(\alpha + \beta = 2\theta\) , and we get:
\[ cos(\alpha + \beta) = cos(\theta + \theta) = cos(\theta)\cdot cos(\theta)\, – sin(\theta)\cdot sin(\theta) \]
And so,
\[ cos(2\theta) = cos^{2}(\theta)\, – sin^{2}(\theta)\,\rightarrow\, sin^{2}(\theta) = cos^{2}(\theta)\, – cos(2\theta)\tag{5} \]
And we have an identity that defines \(sin^{2}(\theta)\) with respect to \(cos^{2}(\theta)\) and \(cos(2\theta)\) (the latter of which is what we want because it is not a squared trigonometric function). And then the fun part where it all sorts itself out, substituting equation (5) into equation (3):
\[ cos^{2}(\theta) = 1\, – sin^{2}(\theta) = 1\, – \left(cos^{2}(\theta)\, – cos(2\theta)\right) = 1\, – cos^{2}(\theta) + cos(2\theta) \]
Then re-arranging:
\[ 2\cdot cos^{2}(\theta) = 1 + cos(2\theta)\,\rightarrow\, cos^{2}(\theta) = \frac{1 + cos(2\theta)}{2} \]
And there we have the identity we need to use to solve the integral for the PDF. Again, while it was possible to just look it up, one of the problems I had in my undergraduate degree is I was given too much “plug and play” math and didn’t get to do any proper mathematical proofs until I was in my 3rd year (and then only because I took an Abstract Algebra elective), and this really caused problems in my 4th years studies where I really needed to understand where the math I was using came from (and how it could be derived). So heading back to the integral of the PDF function:
\[ \int_{-\pi/2}^{\pi/2} A\cdot cos^{2}(\theta’)\, d\theta’ = \int_{-\pi/2}^{\pi/2} A\cdot \frac{1 + cos(2\theta’)}{2}\, d\theta’ = 1 \]
This can be re-written as (bringing the constants to the front):
\[ \frac{A}{2} \int_{-\pi/2}^{\pi/2} \left[1 + cos(2\theta’)\right]\, d\theta’ = \frac{A}{2} \left[\int_{-\pi/2}^{\pi/2} 1\, d\theta’ + \int_{-\pi/2}^{\pi/2} cos(2\theta’)\, d\theta’\right] = 1 \]
We know that the integral of a sum is the sum of the integrals because integration is a linear function (see “Decay and Growth Rates” for more information on this property of integration). We don’t know how to solve the integral of \(cos(2\theta)\), but we do know how to do \(cos(\theta)\) (or \(cos(u)\), which is what will be used), so we can use the substitution technique to tackle this integral. But first, let’s solve the first of the two integrals to get it out of the way:
\[ \int_{-\pi/2}^{\pi/2} 1\, d\theta’ = \int_{-\pi/2}^{\pi/2} \theta’^{\, 0}\, d\theta’ = \frac{1}{0 + 1}\left.\theta’^{\, 0 + 1}\right|_{-\pi/2}^{\pi/2} = \left.\theta’\right|_{-\pi/2}^{\pi/2} = \left(\frac{\pi}{2}\right)\, -\left(-\frac{\pi}{2}\right) = \pi \]
So,
\[ \frac{A}{2} \left[\pi + \int_{\theta’ = -\pi/2}^{\theta’ = \pi/2} cos(2\theta’)\, d\theta’\right] = 1\tag{6} \]
To solve the remaining integral with the substitution method, let \(u = 2\theta’\), therefore:
\[ \frac{du}{d\theta’} = \frac{d}{d\theta’}(2\theta’) = 2\,\rightarrow\, d\theta’ = \frac{du}{2} \]
(if you didn’t understand what just happened, check out “Relativistic energy expansion” ). Now to substitute: a process that has to be done carefully and completely. Looking at the above, we can see that the infinitesimal \(d\theta’\) should be replaced with \(du/2\), and that \(2\theta’ = u\). What is often confusing with the substitution method (at least for me as I was learning) is that the limits of the integral also need to be converted to the new variable (\(\theta’ \rightarrow u\) in this case), which is why I explicitly reminded myself in equation (6) that the limits are specified as \(\theta’\). To convert from \(\theta’\) to \(u\), we have specified \(u = 2\theta’\), so for the upper limit (\(\theta’ = \pi/2\)), \(u = 2\theta’ = 2(\pi/2) = \pi\). Similarly, for the lower limit (\(\theta’ = -\pi/2\)), \(u = 2\theta’ = 2(-\pi/2) =\, -\pi\). The converted function is then:
\[ \frac{A}{2} \left[\pi + \int_{u = -\pi}^{u = \pi} cos(u)\, \frac{du}{2}\right] = \frac{A}{2} \left[\pi + \frac{1}{2}\int_{-\pi}^{\pi} cos(u)\, du\right] = 1 \]
which is an integral that is trivial to do:
\[ \frac{A}{2} \left[\pi + \frac{1}{2}\left.sin(u)\right|_{u = -\pi}^{u = \pi}\right] = \frac{A}{2} \left[\pi + \left(sin(\pi)\, – sin(-\pi)\right)\right] = 1 \]
\[= \frac{A}{2} \left[\pi + \left(0\, – 0\right)\right] = \frac{A\pi}{2} = 1\,\rightarrow\, A = \frac{2}{\pi} \]
Since there is no \(u\) in the value calculated for \(A\), it does not need to be converted back to the variable \(\theta\). Now that we have our normalization constant, substituting it into equation (1) allows us to fully specify the PDF:
\[ f(\theta) = \frac{2}{\pi}\cdot cos^{2}(\theta)\tag{7} \]
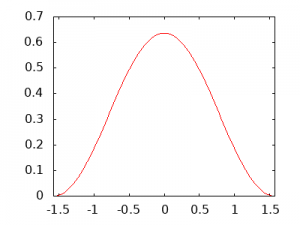
The normalized PDF is shown in the diagram. Note that the only difference is that the peak at \(\theta = 0\) is just lower, but the shape is the same. Somewhat of a slog but hopefully a straightforward one, this is about as easy as integrals get. The next part is also straightforward in terms of math (it’s just a few steps), but it took me a long time to wrap my brain around what was going on. To generate the Cumulative Distribution Function (CDF), you integrate the PDF. The integral starts at the same lower limit; however, instead of using \(\pi/2\) as the upper limit, you use the PDF variable instead (\(\theta\) in this case). What this does is allows some value of \(\theta\) to be plugged into the solved equation, and the answer will be the cumulative integral to that point.
\[ F(\theta) = \int_{\theta’=-\pi/2}^{\theta’=\theta} f(\theta’)\,d\theta’ = \int_{-\pi/2}^{\theta} f(\theta’)\,d\theta’ \]
I specify the overall function, \(F\), as a function of the variable \(\theta\) because the result will be dependent on what value we choose for that variable (it is specified as one of the limits rather as an integration/dummy variable, which is \(\theta’\)). We know from doing the PDF that \(-\pi/2 \leq \theta \leq \pi/2\). We also know that if we integrate over the full range (i.e. setting \(\theta = \pi/2\) when evaluating the integral), we get the answer as 1 (since we normalized the PDF). I hope it is clear that if we set \(\theta =\, -\pi/2\), then the answer of the integral will be 0 (since we’re not actually integrating over any range). Therefore, the possible values of the solution over the range of possible values for \(\theta\) is such that \(0 \leq F(\theta) \leq 1\) because of the way we’ve constructed the PDF so the probabilities over its range will integrate to 100%. Jumping ahead again, if you haven’t realized already, this is how to get the result we are after: if we choose a \(\theta\) and evaluate the integral, we get a number between 0 and 1 inclusive. The computer can generate a random number between 0 and 1, so if we set that as the solution, then we can invert the function and determine which \(\theta\) would give that answer. Because we are using the CDF to do this, the resulting distribution of probabilities will match the \(cos^{2}(\theta)\) distribution we need!
Note that I put primes on the variables involved with the integration part (and left the variables involved with the evaluation part unprimed). This is a reminder that it doesn’t matter what symbol is used when doing an integral, it’s the limits that remain in the solution after they are substituted in after the integration is done.
But first, we need to solve the CDF. We let the solution be \(r\), which represents the “forward” direction for the solution where we specify \(\theta\) and solve for \(r\), but which will be turned backwards after we get a solution so we can specify \(r\) and solve for \(\theta\) (which is called, fittingly, inverting the equation).
\[ F(\theta) = \int_{-\pi/2}^{\theta} f(\theta’)\, d\theta’ = \int_{-\pi/2}^{\theta}\frac{2}{\pi}\cdot cos^{2}(\theta’)\, d\theta’ = r \]
\[ \frac{\pi r}{2} = \int_{-\pi/2}^{\theta}cos^{2}(\theta’)\, d\theta’ = \int_{-\pi/2}^{\theta} \frac{1 + cos(2\theta’)}{2}\, d\theta’ = \frac{1}{2}\int_{-\pi/2}^{\theta} \left[1 + cos(2\theta’)\right]\, d\theta’ \]
Multiplying both sides by 2 and using the linear property of integration:
\[ \pi r = \int_{-\pi/2}^{\theta} 1\, d\theta’ + \int_{-\pi/2}^{\theta} cos(2\theta’)\, d\theta’ = \int_{-\pi/2}^{\theta} d\theta’ + \int_{-\pi/2}^{\theta} cos(2\theta’)\, d\theta’ \]
Solving the leftmost integral and doing the substitution \(u = 2\theta\):
\[ \pi r = \left.\theta’\right|_{-\pi/2}^{\theta} + \frac{1}{2}\int_{-\pi}^{2\theta} cos(u)\, du = \theta\, – \left(-\frac{\pi}{2}\right) + \frac{1}{2}\cdot \left. sin(u)\right|_{-\pi}^{2\theta} \]
\[ = \theta + \frac{\pi}{2} + \frac{1}{2}\left[ sin(2\theta)\, – sin(-\pi) \right] = \theta + \frac{\pi}{2} + \frac{1}{2}\left[ sin(2\theta)\, – 0 \right] \]
Multiplying both sides by 2, simplifying, and re-arranging:
\[ 2\pi r = 2\theta + \pi + sin(2\theta)\,\rightarrow\, 2\pi r\, – \pi = 2\theta + sin(2\theta)\tag{8} \]
Which is our CDF. If we pick a value for \(\theta\), we can use the following equation to easily get an answer for \(r\) between 0 and 1:
\[ r(\theta) = \frac{2\theta + sin(2\theta) + \pi}{2\pi}\tag{9} \]
Giving it a try, for \(\theta = -\pi/2\), \(\theta = \pi/2\), and \(\theta = 0\):
\[ r(\theta = -\pi/2) = \frac{2\cdot(-\pi/2) + sin(2\cdot(-\pi/2)) + \pi}{2\pi} = \frac{-\pi + sin(-\pi) + \pi}{2\pi} = \frac{0}{2\pi} = 0 \]
\[ r(\theta = \pi/2) = \frac{2\cdot(\pi/2) + sin(2\cdot(\pi/2)) + \pi}{2\pi} = \frac{\pi + sin(\pi) + \pi}{2\pi} = \frac{2\pi}{2\pi} = 1 \]
\[ r(\theta = 0) = \frac{2\cdot 0 + sin(2\cdot 0) + \pi}{2\pi} = \frac{0 + sin(0) + \pi}{2\pi} = \frac{\pi}{2\pi} = \frac{1}{2} = 0.5 \]
All of which are the expected answers, so this looks good. Note that the answer \(0.5\) was expected for \(\theta = 0\) because the \(cos^2(\theta)\) function is symmetric around \(\theta = 0\), so integrating it from \(-\pi/2\) to \(0\) will give the same answer as integrating from \(0\) to \(\pi/2\). Therefore integrating to \(0\) will give \(1/2\) of the answer of integrating to \(\pi/2\) (which gives 1).
Lovely. Now, let’s switch it around so if we provide an \(r\) between 0 and 1, we can solve for the \(\theta\) that gives that result. Now here’s one of the reasons why I am doing these solutions: I was lied to. Lied to big time! You might even be in the same position. You see, likely out of necessity and without malice (I hope), all the problems provided to me (and maybe you) as part of my undergraduate degree had analytic solutions (meaning you can you use mathematical symbol manipulation to get an answer). Here, in a process that took many weeks of me thinking I did something wrong with my solutions (repeating the derivation a half-dozen times and getting the same result), or that I was missing some key tool in solving for \(\theta\) in this very simple equation, I discovered the ugly truth: there is no way to solve this equation using any known analytic mathematical technique (or nothing anyone would admit to)! When I went hat in hand for help to a professor I knew, they glanced at it and said “oh, there’s no solution, you’ll have to solve it numerically”. All of the work I did as an undergraduate had not prepared me for this revelation. In fact, most problems can only be solved using either approximation methods, or numerically (hopefully using a computer). I say lie, but it’s more of a lie by omission rather than a direct falsehood (nobody ever told me that all problems could be solved), but it meant I had reached the limits of human knowledge trying to invert what looked to me like a trivial equation. Humbling.
The good news is there are lots of programs that will take an equation with two variables, a value for one of the variables, and can then solve for the other variable numerically. One such package is ROOT, which I mentioned earlier, and was what I had planned to use for my simulation framework anyway. Implementing it in ROOT is not terribly difficult if you know where to look and how to use it. Your mileage may vary, as the saying goes, but it can certainly be learned. Getting a feel for numerically solving this equation is not hard because it can be done with WolframAlpha online. To do it, just enter Equation (9), but instead of using the variable \(r\), you need to specify a number between 0 and 1 inclusive in its place (I also used the variable \(x\) because it’s easier to type, it doesn’t make any difference). The line to type for \(r = 1\) is:
(2 x + Sin[2 x] + Pi)/(2 Pi) == 1
For \(r = 0\):
(2 x + Sin[2 x] + Pi)/(2 Pi) == 0
For \(r = 0.5\):
(2 x + Sin[2 x] + Pi)/(2 Pi) == 0.5
And so on. I ran those in that order and got the answers \(\pi/2\), \(-\pi/2\), and \(0\) respectively (in the section “Solution:” near the bottom of the web page for me). If you are feeling particularly keen to see if it generates a \(cos^2(\theta)\) distribution, you can use the following to generate a random \(r\) and a random \(\theta\) (or \(x\) in this case) from it:
(2 x + Sin[2 x] + Pi)/(2 Pi) == RandomReal[]
You can build a histogram using \(x\) (or \(\theta\)) as your x-axis, dividing up the range (between say \(-1.6\) and \(+1.6\)) into “bins”, and increasing each bin count by one any time the result from the above code falls within that bin. With enough samples, even plotting it by hand on a piece of paper, you will eventually see the \(cos^2(\theta)\) shape taking form. If you do a very large numbers of samples (using a loop and a computer program hopefully), it makes a very nice \(2/\pi\cdot cos^2(\theta)\) distribution. I did this myself with a ROOT program (many tens of thousands of samples) and then overlaid the actual \(2/\pi\cdot cos^2(\theta)\) function, and it was a perfect match. This let me know I wasn’t completely out to lunch on this technique.
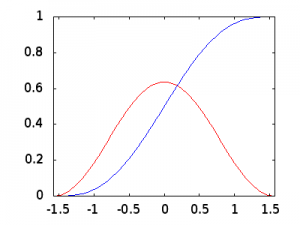
The last question is then: how does this work? If you look at the plot of the CDF over its range from \(-\pi/2\) to \(\pi/2\) (plotted on the x-axis), you can see how the CDF (in blue) increases as we increase the angle towards \(\pi/2\). Each point on the plot is the result from Equation (9), where \(F(\theta)\) (plotted on the y-axis) is calculated for each \(\theta\) value. Comparing it to the normalized PDF (in red), you can see how there’s not much area to integrate on its left, so the CDF increases slowly; but near the middle the PDF is at its maximum and so is the rate of increase of the CDF. Once past \(\theta = 0\), the PDF starts to decrease its height, so the rate of increase of the CDF decreases as it approaches 1 as there is again less to integrate.
Remember that instead of calculating \(0 \leq F(\theta) \leq 1\) when given a \(\theta\) where \(-\pi/2 \leq \theta \leq \pi/2\), we want to calculate \(-\pi/2 \leq \theta \leq \pi/2\) given a \(0 \leq F(\theta) \leq 1\) (which we call \(r\) to remember that we’re randomly generating this number between 0 and 1 inclusive). So, if you look at the CDF plot (in blue), imagine picking a random number between 0 and 1 and drawing a horizontal line across the plot at that y-axis value. Where that line intersects the blue CDF plot line, you draw a vertical line down to the x-axis and that will give you a \(\theta\) value between \(-\pi/2\) and \(\pi/2\) inclusive. But, it’s way easier to “hit” the CDF plot with a horizontal when its slope is high (“hitting the broad side of a barn”, it presents a much larger “target” to horizontal lines from the y-axis along its middle section); but when its slope is lower (e.g. at the bottom and top), there are many fewer chances to hit that section of the plot with a horizontal line if they are randomly distributed along the y-axis (and any \(r\) number has an equal chance of being selected). Because the horizontal lines in the middle of the 0 to 1 range have a higher chance of “hitting” the CDF plot, the chances of an “event” towards the middle of the angular range is much greater. The opposite is true at the edges of the plot. When you generate enough events, their random distribution is uniform in \(r\) but will follow a \(cos^2\) distribution in \(\theta\). And so, using this \(\theta\) distribution will give us the angular distribution we want for our simulated cosmic rays and we have the tricky part for our Monte Carlo simulation ready to roll.
To run the cosmic ray simulation then, I wrote a loop that generated 4 uniform random numbers every pass (each between 0 and 1, with each number equally probable). The first and second were multiplied by 15cm to figure out where the virtual cosmic ray would pass through the upper detector panel (an X coordinate and a Y coordinate). I subtracted 7.5cm from each of the coordinates so the (X,Y) = (0,0) point was in the middle of the upper detector (it made a later calculation easier). The third number was multiplied by \(2\pi\) radians to figure out which compass direction the virtual cosmic ray was coming from. And the fourth number was fed into an equation solver to generate the angle from vertical as a number between \(-\pi/2\) and \(\pi/2\). The four numbers fully specified the trajectory of the cosmic ray through the upper detector panel. Since cosmic rays are so energetic and penetrating (they generally pass through my detector material without hitting any atoms, and bounce off course very little if they do), I just had to project its trajectory in a straight line and figure out what it’s (X,Y) coordinate would be when it intersected the plane of the bottom detector panel (1.0m below the top panel). This was done with basic trigonometry. If the (X,Y) coordinates were each within 7.5cm of the centre of the panel in both X and Y directions, then it was logged as a coincident event (a hit in both panels). From this, I could get a ratio of coincident hits in the detector vs. total cosmic rays hitting the top panel (and would then let me get an expected coincidence count). Running the simulation long enough, I got a good average expected number of coincident cosmic ray events per unit of time. The actual number of physical coincident events I measured in my detector was sufficiently lower than the simulated number that I know that my detector isn’t super duper, but it was still good enough to do the work I wanted to do.
If you have any feedback, or questions, please leave a comment so others can see it. I will try to answer if I can. If you think this was valuable to you, please leave a comment or send me an email at to dafriar23@gmail.com. If you want to use this in some way yourself (other than for personal use to learn), please contact me at the given email address and we’ll see what we can do.
© 2019 James Botte. All rights reserved.
P.S. I used gnuplot running on a CentOS 7 Linux system for the plots. This is the code I used for the last plot:
set yrange[0:1]
set xrange[-pi/2:pi/2]
set terminal png size 400,300
set output 'output.png'
set multiplot
plot 2/pi * cos(x) * cos(x) lt rgb "red"
plot (2*x + sin(2*x) + pi)/(2 * pi) lt rgb "blue"
unset multiplot
Note: When setting the “terminal” to output to PNG image format, gnuplot on my system output (just fyi in case you try and the font looks different):
Options are 'nocrop font "/usr/share/fonts/dejavu/DejaVuSans.ttf,12" fontscale 1.0 size 400,300'
